How well does a mortality table predict Q15 member lifespan?

This is a question people quite reasonably often ask when I blog about which Q15 members are likely to become Church president, using a mortality table as my guide. In this post, I used the same SOA mortality table I’ve been using to forecast longevity, and applied it to Q15 members who have already died, to see how well it predicted when we already know the outcome.

Of course a big weakness of this analysis is that Q15 members aren’t a big group, so it’s hard to say with much certainty how well the table is doing. In order to expand the sample a little, I looked back to all Q15 members who were in their positions in 1950 or who have been called since then, and have since died. For each month of each Q15 member’s life, starting from the later of January 1950 and his calling date, I checked how many actual months of life he had left, as well as what the SOA table said about how much life he had left.

“What the SOA table said” isn’t one number, though, because the table just gives, at each age, the probability of dying in the next year. (It breaks these down by employees and retirees, by women and men, by white collar and blue collar, and by disabled and non-disabled. I always use the white collar non-disabled men, the employees series as long as it goes, and then the retiree series.) What I do is to use these one-year mortality probabilities to find an implied distribution of probabilities of how much more time a man of a particular age has remaining. Really, what I want is just some summary statistics from that distribution: the mean and several percentiles, namely the 5th, the 25th, the 50th (also called the median), the 75th, and the 95th. At the end of the post, if you’re interested, I give a little more detail on this process.

This graph below shows a comparison of what the mortality table predicted versus how long a few Q15 members actually lived. The horizontal axis shows age, and the vertical axis shows years of life remaining. In the lower left, Bruce R. McConkie at age 66 (the left edge of the graph) had fewer than 4 years of life left, as he would die at 69. Cutting through almost the middle of the graph, Gordon B. Hinckley at age 66 had over 30 years left.

 

What’s interesting, of course, is the comparison of these actual life spans to what the mortality table would have predicted. The dashed black line shows the median of the distribution of probability implied by the mortality table at each age. As you can see, it flattens out as age approaches 100, as it always predicts at least a little more life (at least until age 120, where it gives a mortality probability of 100%). I haven’t shown the mean because it’s very similar to the median, falling a bit below it for younger ages, and a bit above it for older ages.

The shaded gray regions are confidence intervals, also from the mortality table. A confidence interval is just a range of values that you think a parameter (in this case, years remaining) falls into. It’s interesting to have a best-guess estimate in the median, but it’s also interesting to have a range of likely values that years remaining falls into. Here, I made the confidence intervals using percentiles from the distribution of probability that I mentioned above. The 50% confidence interval uses the middle 50% of the distribution, so it’s defined using the 25th and 75th percentiles, and the 90% confidence interval uses the middle 90% of the distribution, so it’s defined using the 5th and 95th percentiles.

Of course I can only make these comparison lines for Q15 members who have died. We know that Russell M. Nelson at age 66 had at least 34 years of life left, but maybe he actually had 35 or 37 or 42.

But what you really want to know is how well the mortality table did in predicting lifespans for all the Q15 members, rather than just the few shown in the graph. This table summarizes its performance.

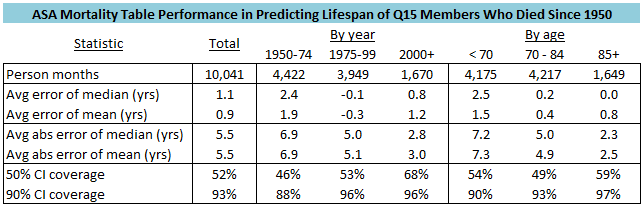
As I said above, at each age from the later of January 1950 or month of calling up through his death, I re-calculated each Q15 member’s actual number of months remaining. With the values from the mortality table, I compared these to the median and the mean, and checked how often the confidence intervals successfully included the actual value (what I’ve called coverage in the table).

The first row in the table tells the number of records there were, so how many person-month calculations I did. Over 10,000 sounds like a lot, but recall that a decade of life for one person is 120 person-months, so this represents data from only a few dozen (37) men. Multiple records for one man are highly correlated with each other, and don’t provide much new information. The second and third rows in the table give the average error in years of using the median or mean to predict each man’s time remaining. Errors are calculated as median (or mean) minus actual value, so positive values indicate the mortality table predicted more time remaining than the man actually had, and negative values indicate it predicted less time remaining than he actually had. The fourth and fifth rows show the average absolute errors. I’ve shown these because while average errors are helpful in seeing the direction of error (i.e., positive or negative), they aren’t as good for seeing the size, since positive and negative errors cancel each other out in the calculation. Average absolute errors give an idea of the magnitude of errors. The last two rows show coverage of the 50% and 90% confidence intervals. If these are performing well, they should successfully include actual values about as often as their stated level of confidence. Finally, the first column in the table shows results for the entire analysis. In the remainder of the rows, I’ve broken results down first by year, and second by age.

Both the median and the mean overestimate Q15 members’ time remaining by an average of about one year. This seems like pretty good performance to me, although I am a bit surprised at the overestimation. Shouldn’t all these men who abstain from alcohol and tobacco live longer than the mortality table averages? But of course, it’s a small sample, and of more importance, it includes some men born a long time ago, some as far back as the late 19th century, who were really living with different standards of medicine and public health than we have today. It shouldn’t be surprising if a sample including such men doesn’t outlive a mortality table from 2014.

In terms of magnitude, both the median and mean error averaged 5.5 years. This seems like pretty good performance to me, as the men are entering the Q15 typically in their 50s or 60s, and almost always have decades of life remaining. A five-year error in predicted life remaining in that context doesn’t seem too bad. Both the 50% and 90% confidence intervals had coverage slightly higher than, but really quite close to, their stated level.

In the year breakdowns, errors generally got smaller, especially in magnitude (absolute value) with increasing Q15 member age. This is probably caused by the fact that there’s a ceiling on human lifespan, and the mortality table knows this, and the age ranges I was looking at here are close to it. This means that when people are older, there is less opportunity to make big errors. When someone is 60, they might die tomorrow when you predicted they’d live to 85 and you make a 25-year error. But when someone is 100, it’s a question of whether they’ll live to 101 or 103. You’re not going to make an error of anything like 25 years.

In the age breakdowns, average absolute error also decreased with time closer to the present. This would make sense given that the mortality table should apply better to people living more recently than it does to some of the older Q15 members. But this is a subset of an already small sample, so it could just be random noise.

Overall, I’m quite impressed with the performance of the mortality table. Like I said, I was a little surprised that Q15 members didn’t outlive the table predictions on average, but I suspect this is just a small sample that includes too many men born a long time ago. I’m especially impressed at the confidence interval performance, and I’m going to have to think of how I might integrate confidence intervals into my future posts about Church president probabilities. I also think it’s encouraging that the average error of the median and mean is only about 20% as large as the average absolute error (about 1 versus about 5). This means that most of the error in one direction is offset by error in the other direction. Ideally, these errors should be as small at possible, but it’s good when at least the predictions miss high to about the same degree that they miss low.

As to the broader question of how seriously you should take the results when I post about Church president probabilities, I don’t think this analysis changes the answer: you shouldn’t take them very seriously. For large groups of people, the mortality table is likely to predict the distribution of their life remaining very well. For a tiny group, or for only one person, it can make big errors. Just look at Russell M. Nelson, who never looked like a good chance to ascend to the presidency in all my past analyses, and then one day he did anyway.

Let me show you one more graph before I wrap up. Life span has been increasing over time even among these already long-lived men. This shows life span by year of death for Q15 members in the sample. I’ve highlighted the shortest-lived man in each 15-year bin because I think it’s interesting how even just this simple measure has been marching relentlessly upward. And this speaks again to the lack of homogeneity in even the little sample I looked at in this post, as the Q15 members born further in the past clearly weren’t living as long on average as those born more recently.

 

__________

Method notes

Here’s an example how I get percentiles from the mortality probabilities in the mortality table. Say I’m looking at an 82-year-old. From the table, his mortality probabilities in the next three years are 4.7%, 5.3%, and 6.0%, respectively. These values in the table are mortality probabilities for people who have reached the start of each year. For example, the 5.3% is only for people who reached age 83. It ignores anyone who died at age 82 (or younger). My problem is that I want to make a distribution that tells me mortality probabilities at all possible future ages for my 82-year-old, without having to assume that he’ll make it to 83, or any other particular age.

Fortunately, it’s straightforward to convert the mortality probabilities from the table into mortality probabilities for an 82-year-old (or for any other selected starting age). For each possible age, I can calculate the person’s probability of dying in that year by multiplying his probability of surviving to that year by his mortality probability (from the table) for that year.

• For his first year, I’ve already said he’s survived to it, so he has a 100% probability of surviving to it, and then a 4.7% probability of dying during it. So his probability of dying during the first year is 100% × 4.7% = 4.7%.
• For his second year, he had a 4.7% probability of dying the previous year, so one minus that, or 95.3% probability of surviving to the second year. Going back to the table, his mortality probability for the second year is 5.3%. So his probability of dying during the second year is 95.3% × 5.3% = 5.1%.
• For his third year, he had a 4.7% probability of dying in the first year and a 5.1% probability of dying in the second, so one minus both of those, or 90.2%, is his probability of surviving to the third year. Going back to the table, his mortality probability for the third year is 6.0%. So his probability of dying during the third year is 90.2% × 6.0% = 5.5%.

After three years, then, an 82-year-old using this table has about a 15% probability of dying (4.7% + 5.1% + 5.5%). To get the percentiles I want (again, it’s the 5th, 25th, 50th, 75th, and 95th), I just stop and note the age when the cumulative percentage reaches the percentage corresponding to the percentile. For the 5th percentile, it’s about 1 year, because there’s a 4.7% probability after 1 year, and 4.7% ? 5%.

To make the whole process more precise, I actually do it at the month level. The mortality table doesn’t have monthly mortality probabilities, but I can calculate them straightforwardly. First, I convert from mortality to survival probabilities by taking one minus the mortality probability. For example, for using the 82-year-old’s table value of 4.7% from above, the survival probability is 1 ? 4.7% = 95.3%. Then, I take the 12th root of the survival probability, which is just the value which when multiplied by itself 12 times will give the yearly survival probability. For the example, it’s 99.6%, because 99.6%₁₂ = 95.3%. This is the monthly survival probability. The 12th root is used because there are 12 months in a year. Finally, I take one minus this monthly survival probability to get the monthly mortality probability, so in the example, 1 ? 99.6% = 0.4%. This process assumes that the probability of survival is the same for all months in a year, which is likely not exactly true, but it’s also probably not too far wrong. The bigger differences are clearly year to year. If monthly differences meant much, the SOA would probably put out a monthly mortality table.

One other question you might be wondering about is why I do the conversion from yearly to monthly probabilities with survival probabilities rather than mortality probabilities. The reason is that they’re easier to work with. Specifically, monthly survival probabilities can be multiplied to get yearly survival probabilities, but the same isn’t true of mortality probabilities. This is because you can get the probability of multiple independent events occurring by multiplying their individual probabilities, and this matches how survival works, where to survive a year, you must survive every single month (it’s like The Not Even Once Club), so it’s easy to calculate a monthly survival probability from a yearly one. The same isn’t true for mortality probabilities.

Getting back to the statistics from the distribution of probabilities, as I said in the post, in addition to the percentiles, I also calculated the mean (or average). To get this, I just used the same process described using the bullet points above (but again, using the more precise monthly calculations). From this process, I had a probability of dying at each possible future age. The probabilities summed up to 1 (or 100%), so the mean was just each age multiplied by its respective mortality probability at that age, and the resulting products summed up. Going back to the example above, this would be 4.7% × 82 + 5.1% × 83 + 5.5% × 84 + . . . to age 120, when the mortality table ends. (If you’re familiar with the idea of a weighted mean, you know that I also needed to divide by the sum of the weights, but as the sum of the weights [i.e., the probabilities] was one, dividing by it had no effect.)